3.5 Counting Subsets

Class: CSE 16 Subject: computer-science discrete-math Date: 2024-10-16 Teacher: Prof. Musacchio

Counting

• If n and k are integers, then $\left(\genfrac{}{}{0ex}{}{n}{k}\right)$ denotes the number of subsets that can be made by choosing $k$ elements from an $n$-element set. We read $\left(\genfrac{}{}{0ex}{}{n}{k}\right)$ as “n choose k.” (Some textbooks write $\mathbb{C}(n,k)$ instead of $\left(\genfrac{}{}{0ex}{}{n}{k}\right)$.)

Example

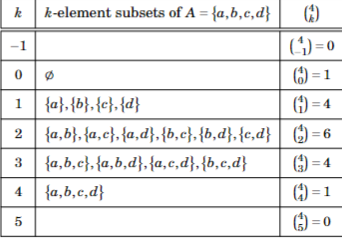
Formula

$\left(\genfrac{}{}{0ex}{}{n}{k}\right)=\frac{n!}{k!(n-k)!}$ $\left(\genfrac{}{}{0ex}{}{n}{k}\right)$ = 0 if: $k<0$ or $k>n$

Example

• How many 5-element subsets of A = {1, 2, 3, 4, 5, 6, 7, 8, 9} have exactly two even elements? Solution
• First select two of the four even elements from A. There are $\left(\genfrac{}{}{0ex}{}{4}{2}\right)$ = 6 ways to do this.
• There are $\left(\genfrac{}{}{0ex}{}{5}{3}\right)$ = 10 ways to select three of the five odd elements of A
• By the multiplication principle, there are \binom{4}{2}$$\binom{5}{3} = 6 · 10 = 60 ways to select two even and three odd elements from A

Example 1

• How many ways are there to deal two 5 card hands and have one leftover pile of 42 cards? Solution $\frac{52!}{5!5!(42)!}=239Trillion$ or

Multinomial Coefficient

$\left(\genfrac{}{}{0ex}{}{52}{5,5,42}\right)$

Example 2

• How many ways to pick a 5 card hand(set) from a 52 card deck so that 47 cards are not in hand? Solution $\frac{52!}{5!47!}=\left(\genfrac{}{}{0ex}{}{52}{5}\right)$ *Note: $\left(\genfrac{}{}{0ex}{}{n}{m}\right)=\left(\genfrac{}{}{0ex}{}{n}{n-m}\right)$

Example 3

• How many 5 card hands consist of a straight flush where the Ace can be considered high or low as needed? Solution

• Let L be the set of all possible card values: L = {2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A}

• Le S be the set of all suits: S = {H, D, S, C}

• 4 ways to pick suit, 10 cards to pick(card value: max at 10) = 40