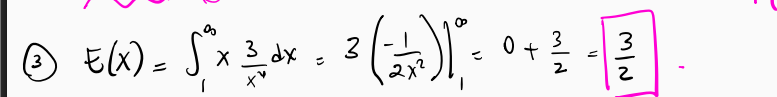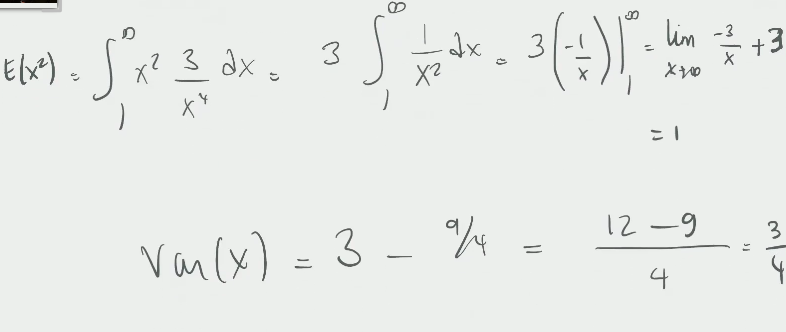Class: STAT 131 Subject: probability Date: 2025-02-11 Teacher: **Prof. Marcela

Continuous Random Variables

• An r.v. has a continuous distribution if its CDF is differentiable. We also allow there to be endpoints (or finitely many points) where the CDF is continuous but not differentiable, as long as the CDF is differentiable everywhere else. A continuous r.v. is a random variable with a continuous distribution.

Examples

• Temperature at a certain location
• Age as a continuous measure: 25 years, 10 months, 2 days, 5 hours, 4 seconds, 4 milliseconds, 8 nanoseconds, 99 picoseconds … and so on.
• Intuition: Things that could take you forever to count

PDF

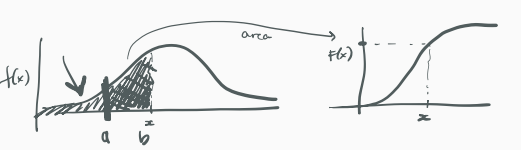
• For a continuous r.v. with CDF , the probability density function (PDF) of is $X$ the derivative of the CDF, given by $f(x)=F^{\prime }(x)$ To go from PDF to CDF, $F(x)={\int }_{-\infty }^{x}f(t)dt$

Visual Representation

Problem 1:

• Let be a continuous random variable with the following PDF

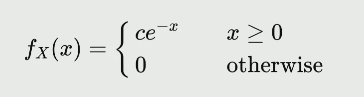
• where c is a positive constant

  • Find $c$
  • Find the CDF of $X$, $F_X(x)$
  • Find $P(1<X<3)$

Expectation

$E(X)={\int }_{-\infty }^{\infty }xf(x)dx$

• Note: may not exist

LOTUS

$E(g(x))={\int }_{-\infty }^{\infty }g(x)f(x)dx$

Uniform Distribution

• denoted by $U$∼$Unif(a,b)$

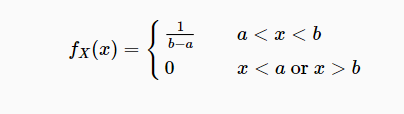
CDF

$F_X(x)=\frac{x}{b-a}$

Expectation

$E(U)=\frac{b+a}{2}$

Variance

$E(U^2)=\frac{(b-a{)}^2}{12}$

Problem 1

• Let X be a continuous random variable with PDF
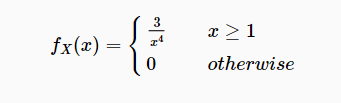
• show that this is a valid PDF
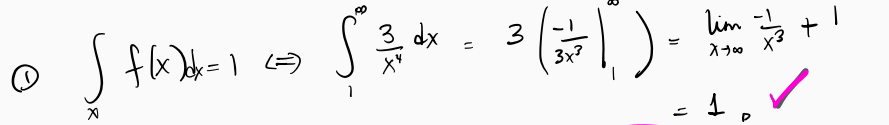
• Find the CDF
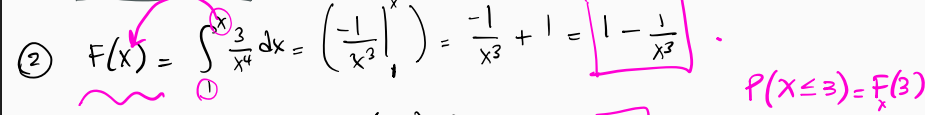
• Find the mean and variance of $X$