Bivariate normal distribution

Class: STAT 131 Subject: probability Date: 2025-03-16 Teacher: **Prof. Marcela

Correlation

Definition

$Corr(X,Y)=\frac{Cov(X,Y)}{\sqrt{Var(x)Var(y)}}$

Scaling has no effect on correlation

Example

1. Let $X$ and $Y$ be two independent $N(0,1)$ random variables and $Z=1+X+Y$, $W=1+X$. Find $Cov(Z,W)$.

$Cov(Z,W)=Cov(1+X+Y,1+X)$ $=Cov(1,1)+Cov(1,X)+Cov(X,1)+Cov(X,X)+Cov(Y,1)+Cov(Y,X)$ since we can’t have the Cov() of a number and a variable, those will get ignored. Therefore: $=Cov(X,X)+Cov(Y,X)$ $=Var(X)+Cov(Y,X)$ $=1+0=1$

2. Let $X$ and $Y$ be two jointly continuous random variables with joint PDF: $f_{XY}(x,y)=2$ for $y+x\le 1,x>0,y>0$ and otherwise. Find and $Cov(X,Y)$ and $p(X,Y)$.

$i)Cov(X,Y)$ $Cov(X,Y)=E(XY)-E(X)E(Y)$ $y+x=1,y=1-x$ $E(XY)={\int }_0^1{\int }_0^{1-x}(2xy)dydx=1/12$ $E(X)={\int }_0^{1}x{f}_x(x)dx$ $f_x(x)={\int }_0^{1-x}{f}_{xy}(x,y)dy={\int }_0^{1-x}2dx=2(1-x)$ $f_y(y)$ is the exact same just $2(1-y)$. Therefore: $E(X)=E(Y)={\int }_0^{1}x2(1-x)dx=1/3$ $Cov(X,Y)=1/12-(1/3)(1/3)=-1/36$

$ii)p(X,Y)$

$p(X,Y)=\frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}}=\frac{-1/36}{Var(X)}$ the reason it’s only Var(X) in the denominator is because before we computed that E(X) = E(Y) which means they will have the same variance.

$Var(X)=E(X^2)-(E(X){)}^2$ $E(X^2)={\int }_0^1{x}^{2}2(1-x)dx=1/6$ $Var(X)=1/6-(1/3{)}^2=1/18$ $p(X,Y)=-1/2$

Bivariate Normal

Definition

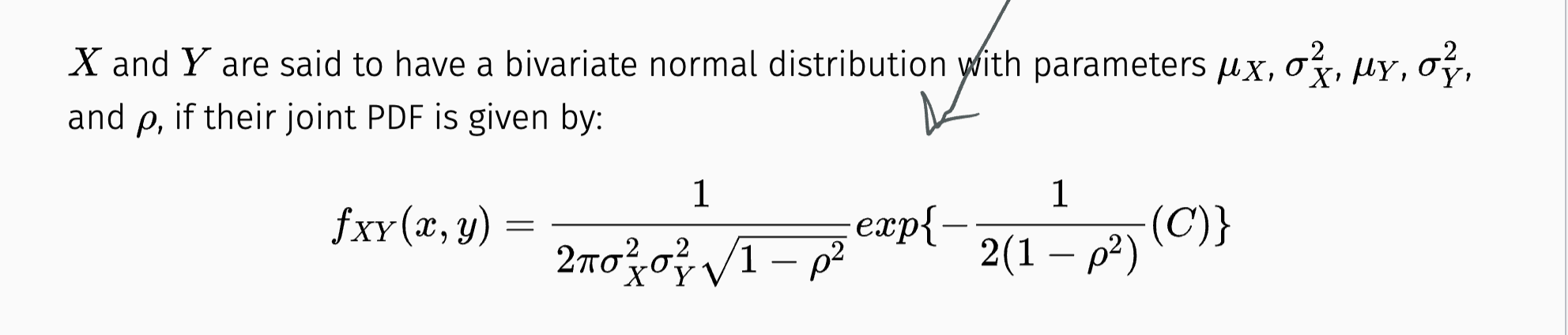
Example

1. Let X and Y be jointly (bivariate) normal, with Var(X) = Var(Y). Show that the two random variables X + Y and X - Y and are independent.

• Since X and Y are jointly distributed and X and Y are normal, we just need to show that $Cov(x+y,x-y)=0$ $Cov(x+y,x-y)=Cov(x,x)-Cov(x,y)+Cov(y,x)-Cov(y,y)$ $=Var(x)-Var(y)=0$

2. 

$i)P(X+Y>0)$

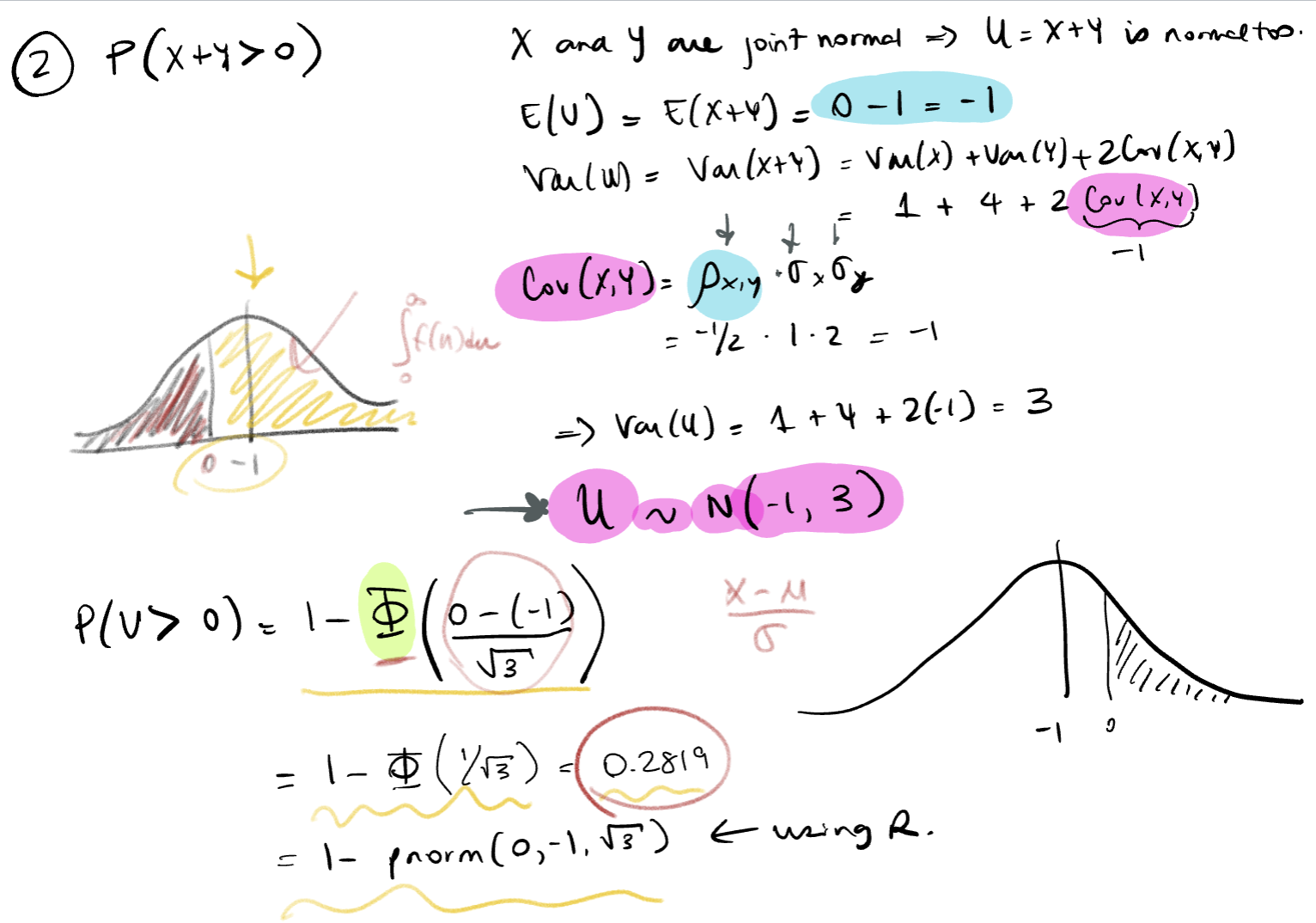
$ii)$ Find a