Heaps Intro

Class: Leetcode Subject: computer-science heaps leetcode Date: 2025-08-15 Teacher: **Gregg Hogg

Heaps/Priority Queues

Operations

1. Heap pop()

• takes out a value from the heap Time Complexity : $O(lo{g}_n)$

2. Heap push()

• pushes a value onto the heap Time Complexity : $O(lo{g}_n)$

3. Heap peak()

• gets the smallest value from the heap Time Complexity : $O(1)$

4. Heapify()

• this initializes the heap. It’s a custom python data structure

Min Heap: Example

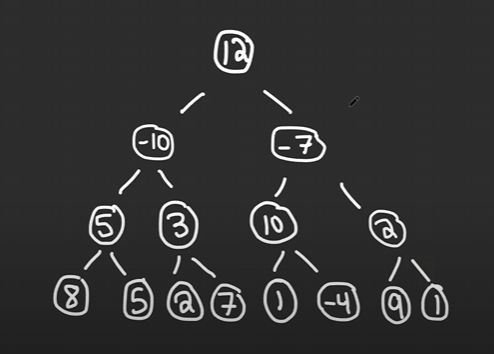
1. This is currently a binary tree

2. We’ll call heapify on it to turn it into a min heap

   1. This will sift down the tree. Essentially it will look at the right most, non-leaf node(2) and check if it’s left or right are smaller. If it is, it will swap with the 2 and so on.

3. The final min heap will look something like this:

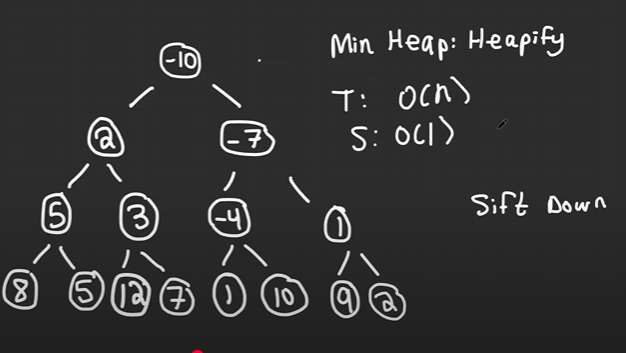
   Time Complexity : $O(n)$ Space Complexity : $O(1)$

Max Heap: Example

• it’s the exact same for min heap except it replaces with the larger value

Building a Min Heap

Min Heap

A = [-4, 3, 1, 0, 2, 5, 10, 8, 12, 9]
 
import heapq
heapq.heapify(A)
 
print(A) # [-4, 0, 1, 3, 2, 5, 10, 8, 12, 9]

Push()

# Heap Push (Insert element)
# Time: O(log n)
 
heapq.heappush(A, 4)
 
print(A) # [-4, 0, 1, 3, 2, 5, 10, 8, 12, 9, 4]

Pop()

# Heap Pop (Extract min)
# Time: O(log n)
 
minn = heapq.heappop(A)
 
print(A, minn) # ([0, 2, 1, 3, 4, 5, 10, 8, 12, 9], -4)

Heap Sort

# Heap Sort
# Time O(n log n)
# Space O(n)
# Note: O(1) Space is possible via swapping, but this is complex
 
def heapsort(arr):
	heapq.heapify(arr)
	n = len(arr)
	res = [0] * n
	
	for i in range(n):
		minn = heapq.heappop(arr) # this will get the smallest element
		res[i] = minn
		
	return res
	
heapsort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0]) # [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]