Ivan's Cool Obsidian Vault

Course Schedule

2 min read

2025-09-18 14:05

Status: child

Tags: leetcode leetcode-medium graphs google Leetcode Graphs Intro computer-science

Course Schedule

Code

from collections import defaultdict
 
class Solution(object):
    def canFinish(self, numCourses, prerequisites):
        """
        :type numCourses: int
        :type prerequisites: List[List[int]]
        :rtype: bool
        """
        # iterative dfs with a stack
 
        g = defaultdict(list)
        courses = prerequisites
        for a, b in courses:
            g[a].append(b)
 
        UNVISITED = 0
        VISITING = 1
        VISITED = 2
        states = [UNVISITED] * numCourses
 
        def dfs(node):
            state = states[node]
            if state == VISITED: return True
            elif state == VISITING: return False
 
            states[node] = VISITING
 
            for nei in g[node]:
                if not dfs(nei): 
                    return False
            
            states[node] = VISITED
            return True
        
        for i in range(numCourses):
            if not dfs(i):
                return False
        
        return True

Explanation

  • The tricky part about this problem is that there could be cycles.
  • To detect cycles, we assign each node one of three possible states
    • UNVISITED (0) → we haven’t explored this node yet
    • VISITING (1) → this node is in the current DFS path (our stack/recursion chain)
    • VISITED (2) → this node and all of its neighbors have already been fully processed
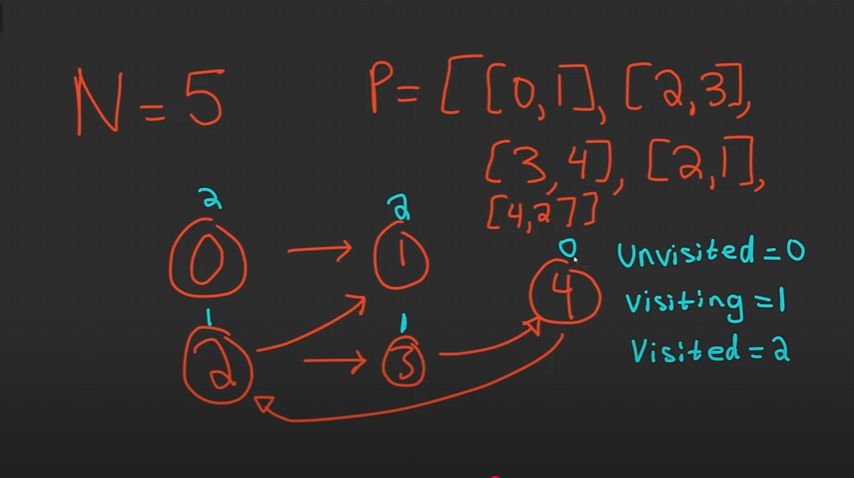
  • The key intuition: if during DFS we ever hit a node that is already in the VISITING state (1), we’ve circled back into our path → meaning there is a cycle → return False immediately.
  • Otherwise, once we finish exploring all neighbors of a node, we can safely mark it as VISITED (2). That way, if we see it again later, we know it has no cycles downstream.
  • We initialize all nodes as UNVISITED in a separate list states. DFS updates this list as it goes.
  • The algorithm simply runs DFS for every course (node). If any of them ever leads to a cycle, we return False. If we finish all without issues, then it’s possible to take all courses → return True.

References

Greg Hogg

Graph View

Backlinks